|
Модели типа реакция-диффузия описывают широкий спектр явлений в физике, химии, биологии, связанных с образованием сложных пространственно-временных структур. Самые разнообразные формы пространственно-временной самоорганизации встречаются в горении (см. работы Я. Б. Зельдовича, А. Г. Мержанова, Г. И. Сивашинского и др.). Многообразие различных видов нелинейных волн включает в себя автомодельные бегущие волны горения, пульсирующие волны горения, ячеистое пламя, радиальные и спиральные волны, образование локализованных очагов горения - горячих точек, которые обладают богатым динамическим поведением, вращающиеся волны, стоячие (или симметричные) волны, сферическое пламя, квазистационарные режимы горения, пространственно-временной хаос и т.д.
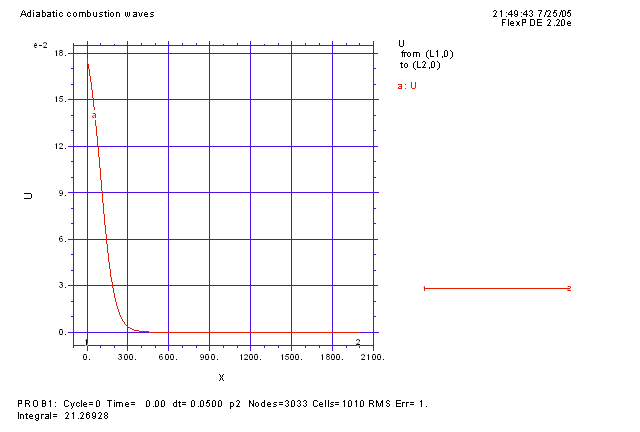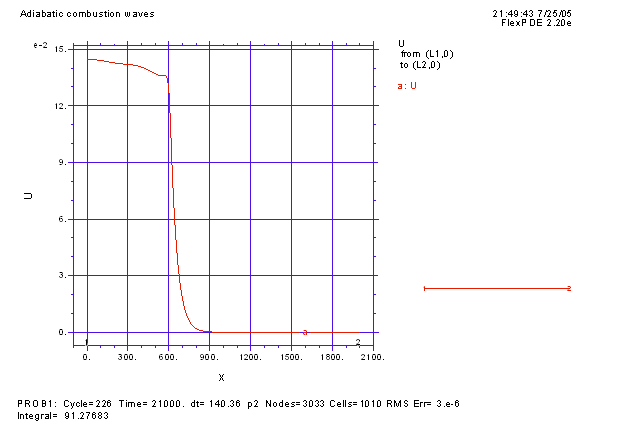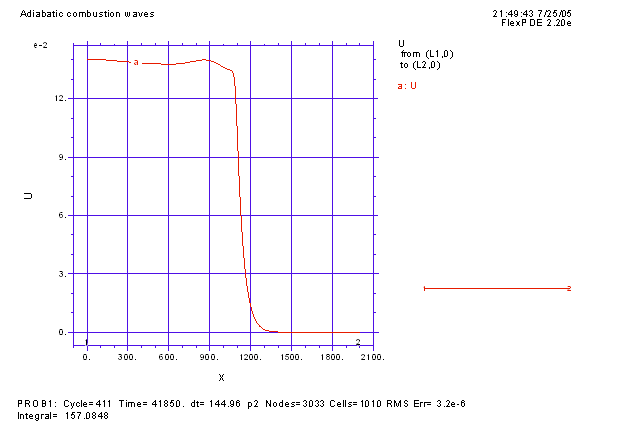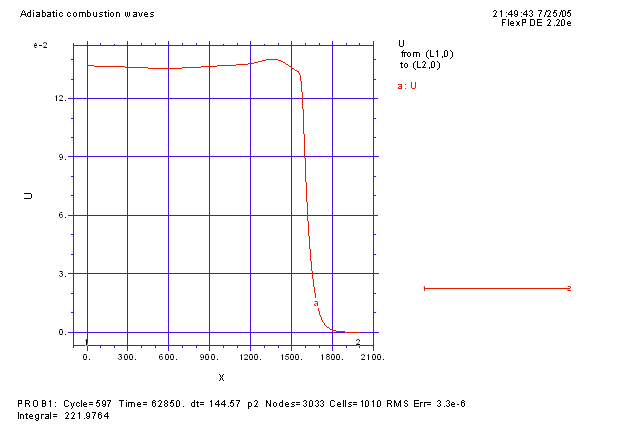
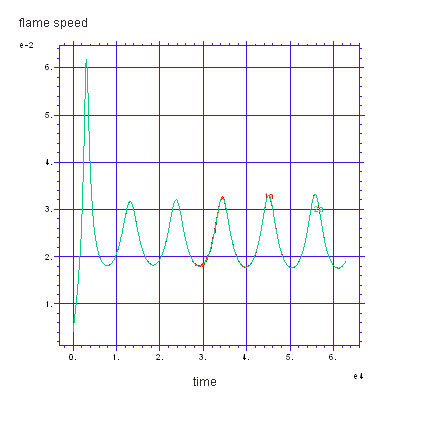
Автомодельная бегущая волна горения распространяться с постоянной скоростью без изменения формы и скорости. Известно, что такие волны могут терять устойчивость при изменении параметров системы. Возникающие при этом неустойчивости могут классифицироваться как продольные или поперечные. Продольные или одномерные неустойчивости связаны с потерей устойчивости в направлении распространения волны и могут проявляться в появлении пульсаций скорости и формы фронта или импульса, что может привести к образованию пульсирующей волны горения. Пример такой волны изображен на рисунке ниже. График представляет собой температуру топливной смеси в одномерном случае. Изначально топливо распределено равномерно по пространству на отрезке от x=0 до x=2000. Волна горения инициируется начальным прогревом топливной смеси на левой границе. Это приводит к формированию пульсирующей бегущей волны, характерезуемой периодической зависимостью как профиля температуры (левый график), так и скорости фронта (правый график) от времени. |
 |
 |
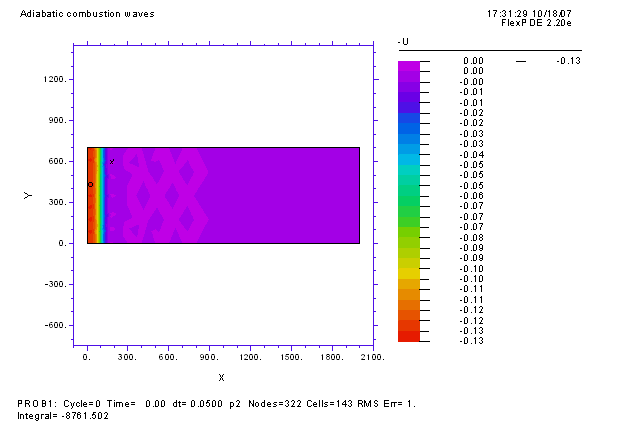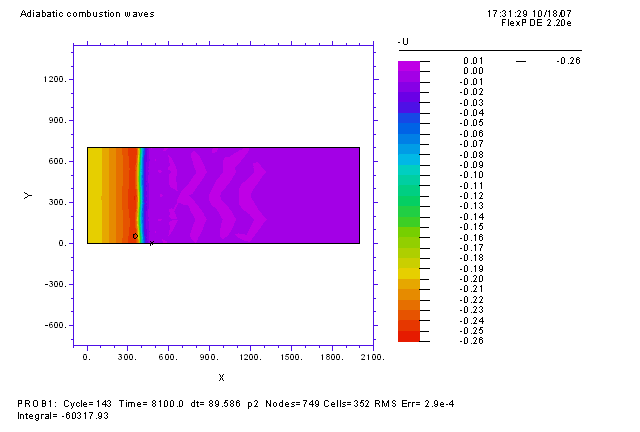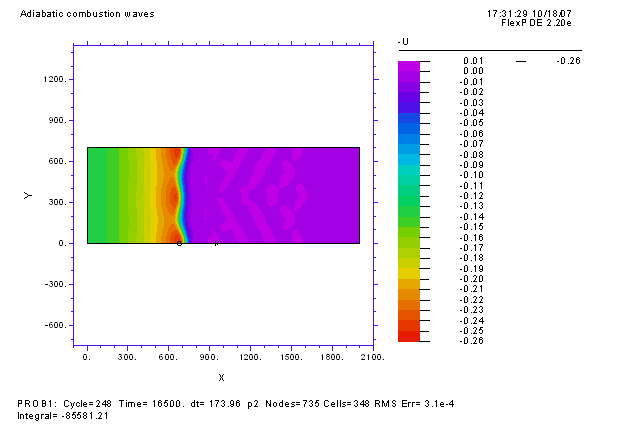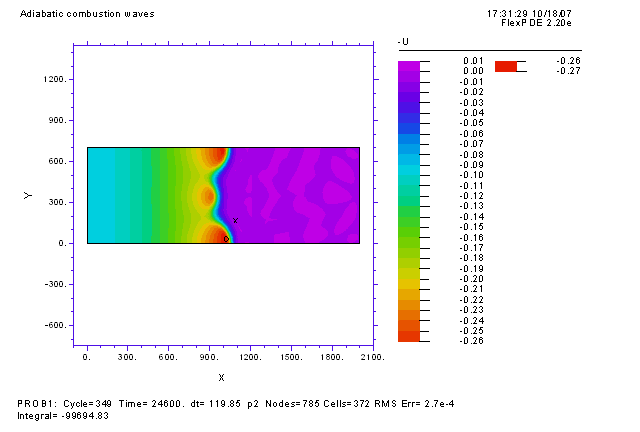
| Поперечные (многомерные) неустойчивости связаны с потерей устойчивости по отношению к возмущениям в направлении поперечном направлению распространения волны и характеризуются определенными волновыми числами. Развитие данного типа возмущений может привести к образованию различных структур в ортогональных распространению волны направлениях. На рисунке ниже изображен контурный график температуры для волны горения, распространяющейся в двумерной области прямоугольной формы. Как и на графиках выше, изначально топливо равномерно распределено по всей прямоугольной области. В начальный момент времени волна горения инициируется равномерным прогревом левой границы (начальный профиль температуры не зависит от y). Это приводит к формированию плоского фронта горения, который начинает распространяться от левой границы (x = 0) к правой границе (x = 2000). Однако развитие поперечной неустойчивости с характерным пространственным периодом по координате y -> Ly ~ 350 приводит к тому, что плоская волна искривляется и разваливается на три ячейки. Отсюда название ячеистое пламя. |
| Комбинированное воздействие продольных и поперечных неустойчивостей может привести к образованию более сложных форм таких как радиальные, стоячие волны, горячие точки и т.д. |

|
| Помимо описанных выше режимов распространения пламени в смесях существуют и более сложные формы такие как хаотическое распространение волны горения. При определенных условиях, развитие продольных неустойчивостей может приводить к тому, что автомодельная волна горения, распространяющаяся с постоянной скоростью, теряет устойчивость в результате первичной бифуркации, а именно, бифуркации Хопфа. В результате образуется пульсирующая волна горения, описанная выше и характеризуемая периодическим во времени изменением скорости и профиля волны. Дальнейшее изменение параметров может привести к вторичной бифуркации - бифуркации удвоения периода, в результате которой пульсации скорости и профилей волны происходят с удвоенным периодом и т.д. Наконец, в результате каскада удвоений периода, сопровождающегося возрастающим усложнением временной динамики системы, рождается хаотический режим распространения пламени. |